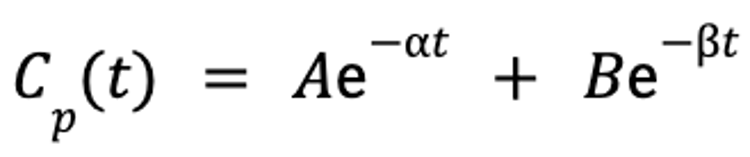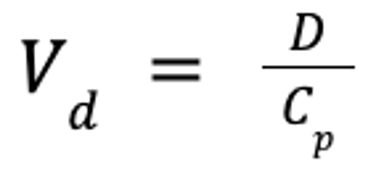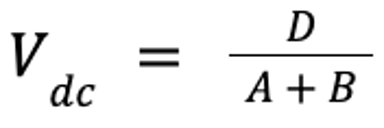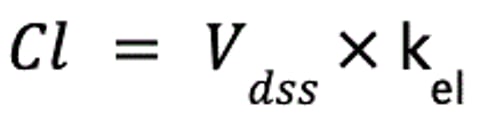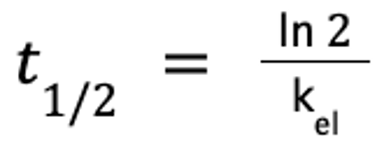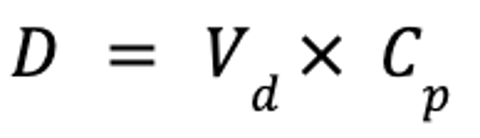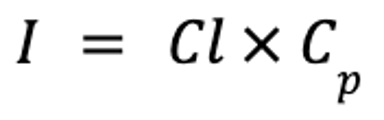Pharmacokinetics is the branch of pharmacology concerned with mathematical description of the time course of plasma drug concentrations measured after administration of a dose. Specifically, pharmacokinetics is the use of mathematical modeling to describe how a drug behaves in the body during absorption, distribution, metabolism, and excretion (together known as ADME). In simple terms, pharmacokinetics describes what the body does to the drug, whereas pharmacodynamics describes what the drug does to the body.
Pharmacokinetic parameters are calculated from plasma drug concentration-versus-time data after a dose of the drug is administered at least via the desired route and ideally also after IV administration (100% bioavailability). The mathematical models developed should enable predictions regarding drug movement in and elimination from the body, so that optimal dosing regimens can be designed, and when necessary, drug withdrawal times (for competition, food safety) can be estimated.
Most pharmacokinetic studies are conducted in healthy animals, yet dosing regimens should be individualized to adjust for differences in physiology (age, sex, species, and breed), pharmacology (drug interactions), and pathology (renal or hepatic disease).
Ideally, the predictions made using pharmacokinetic models are validated in individual patients by the collection of samples for therapeutic drug monitoring. This validation is especially important for drugs with a narrow therapeutic index—ie, a limited range of efficacious tissue concentrations in which concentrations too low are ineffective or concentrations too high are toxic (eg, gentamicin).
The pharmacodynamic response to a drug generally reflects the number of receptors with which the drug interacts (drug-receptor theory). In most instances, tissue drug concentrations parallel plasma drug concentrations, which is why plasma data can usually be used as a substitute for tissue concentrations.
The most relevant pharmacokinetic parameters that describe drug movement and provide the basis for dosing regimens are the apparent volume of distribution (Vd) and the plasma clearance (Cl), both of which determine the elimination rate constant (kel) and elimination half-life (t½). Additional parameters may include the distribution rate constant and distribution half-life and, if the drug is also administered PO, the absorption rate constant and absorption half-life.
After a drug is administered by rapid IV (eg, bolus) injection, the drug will be immediately distributed throughout the central vascular compartment, which includes highly perfused organs. Also immediately, plasma drug concentrations decline due to distribution of drug from plasma into tissues that is faster than the return of drug from tissues to plasma, and elimination from the body (ie, irreversible removal) via metabolism and excretion. Therefore, the decline in plasma drug concentrations initially is rapid; however, after distribution reaches a pseudo-equilibrium such that the amount of drug moving into tissues equals that moving back into plasma, the plasma drug concentration will decline only because of elimination from the body (metabolism and excretion).
With each drug movement, usually a constant fraction or percentage (rather than an amount) moves per unit time (ie, first-order kinetics). Assuming linear pharmacokinetics (direct proportionality between dose and exposure), plasma drug concentrations plotted on a semilogarithmic scale (ie, a logarithmic scale on the y-axis and a linear scale on the x-axis) can be fit by a straight line (suggesting the data are described by a one-compartment pharmacokinetic model) or a biphasic curve (the data are described by a two-compartment model).
In a two-compartment model, the first portion of the concentration-versus-time curve (distribution phase), with a steeper slope, represents distribution and elimination. The terminal portion of the curve (elimination phase), with a flatter slope, represents primarily elimination (ie, distribution of the drug into and out of the tissues is at equilibrium, and distribution into the tissues no longer contributes appreciably to the decline in plasma concentrations).
Macro rate constants can be determined for the distribution and elimination phases through extrapolation back to the y-axis in a process called curve stripping (See plot of two-compartment model). The y-intercept of the line that describes the distribution phase is designated A, and the y-intercept of the line that describes the elimination phase is designated B.
The absolute value of the slope of the elimination phase is the elimination rate constant (often referred to as beta or kel), and from it is derived the elimination half-life (t1/2).
The absolute value of the slope of the line that describes the distribution phase is the called the distribution rate constant (often referred to as alpha or kd). This rate constant enables calculation of a distribution half-life.
Once the data are mathematically described by the slopes and y-intercepts of these lines, the plasma drug concentration at any given time point after the drug is administered can be predicted by the following equation:
where Cp(t) is the plasma concentration as a function of time, A is the y-intercept of the line that describes the distribution phase, α is the rate constant for the distribution portion of the plasma concentration-versus-time curve, B is the y-intercept of the line that describes the elimination phase, β is the rate constant for the elimination portion of the plasma concentration-versus-time curve, e is the base of the natural logarithm, and t is the time since administration.
From these models, clinically relevant parameters (Vd and Cl) can be calculated and used to determine appropriate dosing regimens.
Apparent Volume of Distribution
The pharmacokinetic parameter used to assess the extent of drug distribution throughout the body is known as the apparent volume of distribution (Vd). If both the dose and plasma drug concentration are known, then Vd can be calculated as follows:
where Vd is the apparent volume of distribution (in L/kg), D is the dose (in mg/kg), and Cp is the plasma drug concentration (in mg/L).
This theoretical volume is the volume into which the drug must be distributed if the concentration in plasma represents the concentration throughout the body. The term "apparent" underscores the fact that Vd does not indicate where the drug is distributed, but only that it goes somewhere.
There are several ways to calculate Vd, depending on the drug and clinical need. For injectable anesthetic agents, the concentration in the central, or vascular, compartment (which includes the brain and highly perfused organs) is the most important because this concentration most likely reflects the concentration of the anesthetic agent in the brain. In this case, Vd of the central compartment (Vdc) can be estimated:
For most other drugs, Vd at steady state (Vdss), which reflects the volume that appears to be occupied when tissue distribution reaches pseudo-equilibrium, is calculated by summing Vdc and the theoretical volume of the second tissue compartment (V2). V2 is calculated from the rate constants estimated by mathematical modeling software during the data-fitting process.
Vd is useful for several reasons. Perhaps most importantly, it can be used to calculate a dose if the target Cp is known, by rearrangement of the equation for Vd. For example, if the steady-state Vd (Vdss) of phenobarbital is 0.6 L/kg, and the target concentration of phenobarbital in a drug-naive animal is 10 mg/L, the IV dose is calculated as follows:
This is especially useful for calculating loading doses for anesthetic agents; however, Vdc should be used for that purpose.
An additional reason Vd is useful is that if Cp is known at any time after the dose is administered, then Vdss can be used to calculate how much drug is left in the body.
Finally, Vdss can be used to predict the relative ability of the drug to move to different body compartments. If limited to the extracellular compartment (interstitial fluid, plasma), as is typical of water-soluble drugs, the drug represents 20%–30% of body weight, and the Vd of such a drug should be < 0.3 L/kg.
Lipid-soluble drugs are generally able to penetrate cell membranes and thus are distributed to both extracellular and intracellular fluid, which represents ~60% of the body weight. Such drugs are generally characterized by Vd > 0.6 L/kg. Some drugs are limited to the plasma compartment and do not distribute well. For example, for drugs very tightly bound to plasma proteins, Vd approximates the size of the blood compartment, or < 0.1 L/kg. As the drug is freed from the protein, however, it will leave the plasma compartment and distribute into tissues.
Many drugs are characterized by a Vd that exceeds the body weight of the animal (ie, > 1 L/kg). For example, the mean digoxin Vd in dogs is 13 L/kg. This means that digoxin binds appreciably in other tissues (ie, if the drug leaves the plasma, regardless of where it goes, Vd will increase).
The Vdss of a drug is usually consistent over a wide dose range for a given species, and it is the best estimate of Vd for extrapolating across species. However, a number of clinically important factors can influence Vd, including age (Vd is larger in neonates and pediatrics, smaller in geriatrics); functional status of the kidneys (Vd is decreased with dehydration), liver (Vd is increased with edema), and heart; fluid accumulations; concentration of plasma proteins (influencing unbound drug only); acid-base status (particularly if ion trapping causes the drug to accumulate in tissues); inflammatory processes or necrosis (tends to increase distribution); and any other causes for alteration in the extent of plasma-protein binding.
Drug Clearance
As soon as a drug reaches the systemic circulation, it immediately begins to be cleared from plasma. Clearance is the volume of blood from which a drug is irreversibly eliminated, or cleared. Usually plasma is sampled; however, plasma clearance represents the sum clearances by all organs. If the drug is cleared by only a single organ, then plasma clearance is the clearance of that organ.
An alternative definition of clearance is the volume of plasma that would contain the amount of drug excreted per unit time. This definition demonstrates the link between volume of distribution (Vd) and clearance. If the elimination rate constant (kel) is known, it describes the fraction of Vdss cleared, and together, these two values can be used to calculate clearance:
where Cl is clearance (in mL/kg/min), Vdss is the apparent volume of distribution at steady-state (in mL/kg), and kel is the elimination rate constant (in min−1).
Like Vd, then, Cl directly influences kel, the rate at which drug is eliminated from the body: as Cl increases, kel becomes steeper. Clearance is independent of the Vd of a drug and thus of the concentration of drug in the blood; no matter how much drug is in the blood, the same volume will be cleared per unit time.
The two major organs responsible for clearance are the liver and kidneys. After a drug is metabolized, it is irreversibly eliminated from the body. Its metabolites, however, must be excreted (usually by the kidneys).
Hepatic clearance is defined as the volume of plasma totally cleared per unit time as blood passes through the liver. The rate of hepatic clearance depends on drug delivery to the liver—ie, blood flow (Q) and the extraction (E) ratio of the drug, or fraction of the drug removed as it passes through the liver. Extraction, in turn, is determined by the intrinsic clearance (metabolic capacity) of the liver.
Drugs cleared by the liver fall into two major categories. Flow-limited drugs are extracted so rapidly that Q becomes the limiting factor of hepatic clearance. Binding to plasma proteins will not influence the clearance of such drugs.
In contrast, the rate-limiting step of capacity-limited drugs is intrinsic clearance, the metabolic capacity of the liver. For such drugs, binding to serum proteins will decrease the rate of clearance. Therefore, highly protein-bound drugs are referred to as "capacity limited, binding sensitive," as opposed to drugs not highly protein bound and thus "capacity limited, binding insensitive."
Hepatic disease differentially impacts flow- and capacity-limited drugs. Hepatic clearance of flow-limited drugs markedly decreases with changes in hepatic blood flow, such as might occur with portosystemic shunting. When administered PO, such drugs are normally characterized by high first-pass metabolism and low oral bioavailability. With portosystemic shunting, oral bioavailability can markedly increase, so oral doses must be decreased in proportion to the extent of shunted blood. Changes in hepatic mass and function will affect capacity-limited drugs. In general, if liver disease has negatively affected serum albumin and BUN concentration, the intrinsic metabolic capacity of the liver is also likely to be negatively affected. However, if protein-binding decreases for a highly protein-bound drug such that more of the drug is unbound, hepatic clearance may not be as negatively affected.
Renal clearance is defined as the volume of plasma totally cleared of a drug per unit time (eg, L/min) during passage through the kidneys. The renal clearance of drugs depends primarily on renal blood flow; it is also affected by urine pH, extent of plasma-protein binding, urine-concentrating ability, and concomitant use of certain drugs.
Serum creatinine concentration or serum creatinine clearance can be used to assess changes in renal clearance as renal function declines. Either the dose or the interval can be proportionately modified. For drugs with a short half-life, intervals are more appropriately prolonged (compared with decreasing dose) as serum creatinine concentration increases; for drugs that accumulate because of a long half-life, the dose or interval might be proportionately decreased or prolonged, respectively.
Elimination Rate Constant
The elimination half-lifeis the time that lapses as Cp decreases by 50%.
The elimination half-life is derived from the elimination rate constant, kel, which is the slope of the terminal component of the plasma concentration-versus-time curve. A hybrid parameter, kel is affected by both Cl and Vd. Cl determines the rate of decline in Cp; thus, the greater the volume of drug cleared, the steeper the slope, or kel. The impact of Vd on half-life reflects its effect on Cp: a larger Vd means that less drug is in the volume of blood cleared by the liver or kidneys. Therefore, the rate of elimination declines as Vd increases, resulting in an inverse relationship.
The elimination half-life is calculated as follows:
where ln 2 ≈ 0.693.
The relationship between kel and t1/2 reflects the fact that t1/2 becomes the run of the slope as concentration decreases by 50% (ie, C1/C2 = 2, where C1 is the concentration at time 1 and C2 is the concentration at time 2). Because t1/2 is inversely proportional to kel, t1/2 is directly proportional to Vd (larger Vd results in a longer half-life) and inversely proportional to Cl.
Note that Cl and Vd can be profoundly altered, yet t1/2 may not change. For example, in an animal dehydrated because of renal dysfunction, Cl may be decreased by 50%, thereby doubling t1/2. If the animal is markedly dehydrated, however, then Vd will decrease because of the contraction of extracellular fluid volume. Because more drug is in each milliliter of blood cleared by the kidney, the same amount of drug may be eliminated, and thus kel or t1/2 may not change.
The elimination half-life determines the amount of time to steady state and the amount of time for a drug to be eliminated from the body after drug administration is discontinued. After a drug is discontinued, 50% of it is eliminated after one half-life, 75% after the second half-life (half of 50%), 87.5% after the third, and so on. For practical purposes, most of the drug is eliminated by 3–5 half-lives.
The elimination half-life, along with tolerances, determines withdrawal or milk discard times in food animals and withdrawal times for animals competing in regulated sporting events. The relationship between dosing interval and elimination half-life also determines whether a drug will fluctuate or accumulate during a dosing interval.
Single-Dose Concentration Curves After Extravascular Administration of Drugs
When a drug is administered by an extravascular route, plasma drug concentrations rise until a peak or maximum drug concentration (Cmax) is reached. After the drug enters circulation, it is subjected immediately and simultaneously to distribution, metabolism, and excretion. The plasma concentration-time curve after extravascular administration has an additional y-intercept and slope, and the slope reflects the absorption rate constant, ka. The absorption half-life is the time that elapses as 50% of the drug is absorbed into the system. Absorption generally is sufficiently slow that drug distribution is generally masked by the absorption phase. Therefore, as plasma drug concentrations decline after Cmax is reached, the slope generally reflects kel.
The term bioavailability is used to express the rate and extent of absorption of a drug.
Steady-State Plasma Concentration (Repeated Administration or Constant IV Infusion) of Drugs
In some cases, the desired therapeutic effect of a drug is produced with a single dose. To achieve a satisfactory response, however, it is frequently necessary to maintain drug concentrations in the therapeutic range for a longer time. Rather than administering large doses, which could result in potentially toxic plasma drug concentrations, multiple dosing allows regular, safer intervals. For drugs with a very short half-life, the drug may be administered through a catheter as a constant-rate infusion, which is essentially continuous IV delivery. The rate of administration depends on the amount of fluctuation in drug concentration that can occur during a dosing interval, which in turn is determined by the relationship between t1/2 and the dosing interval, Τ.
If a drug is administered at an interval substantially longer than its half-life, most of the drug will be eliminated during each dosing interval. Therefore, little drug remains when the subsequent dose is administered, and plasma drug concentrations will fluctuate (from maximum drug concentration [Cmax] to the minimum drug concentration [Cmin]) during the dosing interval.
For example, if a drug with a 4-hour half-life is administered every 12 hours, 87.5% of the drug will be eliminated during each dosing interval. With each dose there is a risk that drug concentrations will become subtherapeutic; increasing the dose will result in a small increase in Cmin but may substantially increase Cmax, thus increasing the risk of toxicosis.
A more appropriate response would be to decrease the dosing interval. However, this may be necessary only if drug efficacy depends on the presence of the drug. For example, this amount of fluctuation may be acceptable for a concentration-dependent antimicrobial such as gentamicin. If the drug is an anticonvulsant, however, the risk of seizures increases just before the next dose. If the drug is time dependent, drug concentrations may decrease to below the minimum inhibitory concentration of the infecting microbe.
In contrast to drugs with a short half-life, drugs with a long half-life compared with the dosing interval will accumulate with each dose because much of the drug remains in the body when the next dose is administered. Drugs with a long half-life begin to accumulate with the first dose and continue to do so until a steady-state equilibrium is reached such that the amount of drug eliminated during each dosing interval is equivalent to the amount of drug administered during that same interval. The accumulation ratio describes the magnitude of increase of either Cmax or Cmin at steady state compared with the first dose. The longer the half-life is compared with the dosing interval, the greater the accumulation ratio is.
As with drug elimination, for practical purposes, steady state is achieved within 3–5 half-lives, regardless of the drug or dose, provided the preparation and dosing regimen are the same. In such cases, 50% of the plateau or steady-state concentration will be reached after 1 half-life, 75% after 2 half-lives, 87.5% after 3 half-lives, and 93.6% after 4 half-lives. Response to the drug, whether efficacy or toxicosis, cannot be assessed until steady state is reached. Because the amount of drug in the body is large compared with each dose, manipulating plasma drug concentrations for such drugs is difficult, because changes require dosing for 3–5 half-lives at the new dose.
If the time to reach steady state, and thus time to therapeutic effect, is unacceptable, steady-state plasma drug concentrations may be achieved more rapidly by administration of a loading dose or doses, as follows:
where D is the dose (in mg/kg), Vd is the volume of distribution at steady-state (in mL/kg), and Cp is the target plasma concentration (in mg/mL). If the drug is administered PO, the dose must account for bioavailability:
where F is the bioavailability (in %). However, the drug will not be at steady state, but only at steady-state concentrations.
If the maintenance dose does not maintain what the loading dose achieved, then as steady state at the maintenance dose is reached, plasma drug concentrations may increase to cause toxicosis or decrease to a subtherapeutic concentration.
Drugs with very short half-lives are often administered by constant-rate infusions in animals in critical condition. In such cases, the interval is infinitely short compared with the half-life, and the drug accumulates until steady state is reached. The rate of infusion can be calculated as follows:
where I is the rate of infusion (in mcg/kg/min), Cl is clearance (in mL/kg/min), and Cp is the target plasma concentration (in mcg/mL).
A loading dose should be administered if the time to steady state is unacceptably long.